A Fractal Field Guide
This is a collection of limit sets rendered mostly between Jan'93 and Apr'94 using
a program that I was developing with the working title Live Fractal.
These pictures differ from the usual fractals you see in a few regards
- the defining mathematical formula come from families much more general than
the ones for Julia and Mandelbrot sets
- the pictures are rendered using inverse iteration as opposed to escape time
algorithms. As a result, only the limit sets themselves are shown, without
the razzle dazzle of a surrounding color field.
- the inverse iteration algorithm is able to handle not only the usual
IFS and Julia fractals, but also the limit sets of Kleinian groups, as
popularized in the book
Indra's Pearls.
In the list below, the accompanying descriptions are probably
vague and unhelpful, but should give an impression of the wide variety of
fractal types possible.
The rendering method used is in spirit the same as that popularized by Barnsley
for his IFS fractals. Many of the images have color which indicates the
number of times the algorithm visited a given region. Black indicates a
few hits, green some more, and red and yellow indicate many hits. Like photography,
the images you get depend on exposure time and filters. The series of images
presented here are more like polaroid snapshots than serious attempts at
creating high quality pictures.
Quadratic Rationals (including matings)
-
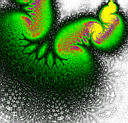
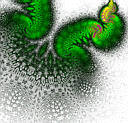
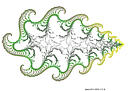
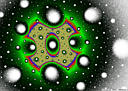 - inverse quadratic
- inverse quadratic
-
 - inverse quadratic
- inverse quadratic
-
 - a quadratic mating (rabbit+peapod)
- a quadratic mating (rabbit+peapod)
-
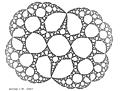 - a quadratic mating (rabbit+basilica)
- a quadratic mating (rabbit+basilica)
-
 - a quadratic self-mating (peadpod+peapod)
- a quadratic self-mating (peadpod+peapod)
-
 - a quadratic mating
- a quadratic mating
-
 - quadratic self mating
- quadratic self mating
-
 - inverse quadratic
- inverse quadratic
-
 - quadratic rational
- quadratic rational
-
 - quadratic rational
- quadratic rational
-
 - quadratic rational
- quadratic rational
-
 - quadratic rational
- quadratic rational
-
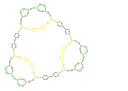 - inverse quadratic
- inverse quadratic
-
 - inverse quadratic
- inverse quadratic
Carpet Fractals
-
 - cubic version of a carpet fractal
- cubic version of a carpet fractal
-
 - a carpet fractal
- a carpet fractal
-
 - a carpet fractal
- a carpet fractal
-
 - almost a carpet fractal
- almost a carpet fractal
-
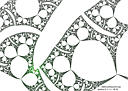 - a close-up of RABBIT
- a close-up of RABBIT
-
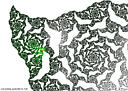 - a carpet fractal closeup
- a carpet fractal closeup
Conformal Maps and Correspondences
-
 - derived from Barnsley's foggy coastline
- derived from Barnsley's foggy coastline
-
 - generated by Gauss's Arithmetic-Geometric mean algorithm
- generated by Gauss's Arithmetic-Geometric mean algorithm
-
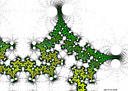 - generated by Gauss's Arithmetic-Geometric mean algorithm
- generated by Gauss's Arithmetic-Geometric mean algorithm
-
 - a quadratic correspondence
- a quadratic correspondence
-
 - a quadratic correspondence
- a quadratic correspondence
-
 - a perturbation of a mapping whose symmetry group is a dihedral group
- a perturbation of a mapping whose symmetry group is a dihedral group
-
 - two superimposed members of a circle inversion group
- two superimposed members of a circle inversion group
-
 - group of Moebius transformations
- group of Moebius transformations
-
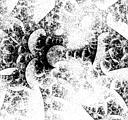 - group of Moebius transformations
- group of Moebius transformations
-
 - a quadratic correspondence
- a quadratic correspondence
-
 - not a fractal, but the image of a grid under an iterated conformal map
- not a fractal, but the image of a grid under an iterated conformal map
-
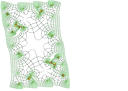 - see CONFORM2
- see CONFORM2
-
 - not a fractal, but the image of a circle under an iterated conformal map
- not a fractal, but the image of a circle under an iterated conformal map
Kleinian Groups
-
 - a Kleinian group whose limit set consists of circles
- a Kleinian group whose limit set consists of circles
-
 - a Schottky group
- a Schottky group
-
 - a Schottky group (verging on quasi-fuchsian)
- a Schottky group (verging on quasi-fuchsian)
-
 - a Schottky group
- a Schottky group
-
 - a Schottky group, showing the 4 generating circles
- a Schottky group, showing the 4 generating circles
-
 - a Kleinian group
- a Kleinian group
-
 - a nearly quasi-fuchsian group
- a nearly quasi-fuchsian group
-
 - a quasi-fuchsian group
- a quasi-fuchsian group
-
 - partial rendering of a quasifuchsian group limit set
- partial rendering of a quasifuchsian group limit set
-
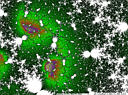 - 10. quasi-fuchsian limit set - this is actually a nearly plane-filling curve. This picture was used in the book
The Honors Class, by Ben Yandell
- 10. quasi-fuchsian limit set - this is actually a nearly plane-filling curve. This picture was used in the book
The Honors Class, by Ben Yandell
-
 - 11. A zoomed out version of 10. The box shows where 10 is situated.
- 11. A zoomed out version of 10. The box shows where 10 is situated.
-
 - 12. Same as 11, shows isometric circles
- 12. Same as 11, shows isometric circles
-
 - 13. a zoomed out version of 11. Note that peripheral resolution degrades.
- 13. a zoomed out version of 11. Note that peripheral resolution degrades.
-
 - 14. Zoomed out 13
- 14. Zoomed out 13
-
 - the limit set in 10-14 rendered as a curve.
- the limit set in 10-14 rendered as a curve.
-
 - the limit set in 10-14 rendered as a curve (zoomed out)
- the limit set in 10-14 rendered as a curve (zoomed out)
-
 - the limit set in 10-14 rendered as a curve(zoomed out even more)
- the limit set in 10-14 rendered as a curve(zoomed out even more)
-
 - in the neighbourhood of the Riley slice of Schottky space
- in the neighbourhood of the Riley slice of Schottky space
-
 - a Schottky group with 4 generating circles shown
- a Schottky group with 4 generating circles shown
-
 - an outlying Schottky group
- an outlying Schottky group
Non-Conformal Maps
-
 - a non-conformal function
- a non-conformal function
-
 - a conjugate quadratic
- a conjugate quadratic
-
 - a non-conformal function
- a non-conformal function
-
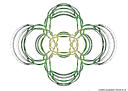 - a non-conformal function
- a non-conformal function
-
 - a nonconformal map (verging on strange attractor)
- a nonconformal map (verging on strange attractor)
Glynn Sets
Quadratic and Cubic Julias
-
 - a quadratic Julia set
- a quadratic Julia set
-
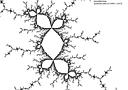 - a dendritic rabbit
- a dendritic rabbit
-
 - a cubic Julia set
- a cubic Julia set
-
 - a cubic Julia set
- a cubic Julia set
-
 - a cubic Julia set
- a cubic Julia set
-
 - a cubic Julia set
- a cubic Julia set
-
 - a cubic Julia
- a cubic Julia
-
 - a cubic Julia
- a cubic Julia
-
 - a quadratic Julia
- a quadratic Julia
-
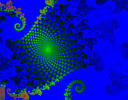 - a quadratic Julia set
- a quadratic Julia set
-
 - a quadratic Julia set (same as JULIA2, but with a white background)
- a quadratic Julia set (same as JULIA2, but with a white background)
-
 - Julia set for z^10+c
- Julia set for z^10+c
back to my home page
 - inverse quadratic
- inverse quadratic  - inverse quadratic
- inverse quadratic  - a quadratic mating (rabbit+peapod)
- a quadratic mating (rabbit+peapod)  - a quadratic mating (rabbit+basilica)
- a quadratic mating (rabbit+basilica)  - a quadratic self-mating (peadpod+peapod)
- a quadratic self-mating (peadpod+peapod)  - a quadratic mating
- a quadratic mating  - quadratic self mating
- quadratic self mating  - inverse quadratic
- inverse quadratic  - quadratic rational
- quadratic rational  - quadratic rational
- quadratic rational  - quadratic rational
- quadratic rational  - quadratic rational
- quadratic rational  - inverse quadratic
- inverse quadratic  - inverse quadratic
- inverse quadratic